XSHELL
PAPER SHELL MADE OF CELL UNIT
ELECTIVE COURSE, FALL '19, CORNELL UNIVERSITY
IN COLLABORATION WITH YU SUN, MENGYI YAN, AND JUNSIK OH
XSHELL
PAPER SHELL MADE OF CELL UNIT
ELECTIVE COURSE, FALL '19, CORNELL UNIVERSITY
IN COLLABORATION WITH YU SUN, MENGYI YAN, AND JUNSIK OH
This project explores the simplest way of constructing a doubly-curved shell structure - by setting the fabrication method based on planar manufacture, which can be achieved by CNC Routers or laser machines and using sheet materials like chipboard. The cellular unit was mapped and unrolled to planar folding and cutting lines, fabricated through tens of recycling chipboards within 2mm thickness. The whole fabricating process including cutting, folding, and assembling took only 5 days and 3 group members to complete the construction of this human-scale installation on the 3rd floor of Sibley Hall.
This project explores the simplest way of constructing a doubly-curved shell structure - by setting the fabrication method based on planar manufacture, which can be achieved by CNC Routers or laser machines and using sheet materials like chipboard. The cellular unit was mapped and unrolled to planar folding and cutting lines, fabricated through tens of recycling chipboards within 2mm thickness. The whole fabricating process including cutting, folding, and assembling took only 5 days and 3 group members to complete the construction of this human-scale installation on the 3rd floor of Sibley Hall.
ARCHITECTURAL GEOMETRY
Fabrication-Oriented Topological Geometric Optimization of Complex Spatial Structures
INDEPENDENT RESEARCH, 2021
CO-AUTHORING WITH XIANG WANG
In this paper, the interaction and feedback between the architectural/structural design requirements and the constructional/geometric constraints are analyzed using the surface topology polygon mesh structure as the medium. Meshing is a common issue in the design of architectural surfaces. Both architectural and structural requirements often directly affect the layout and direction of the grid. At the same time, the special geometric properties of the grid can make it meet the fabrication constraints of different conditions, and may also affect the final form and the structural analysis at the same time. This paper explores the confrontation and balance between structural requirements and fabrication constraints in the architectural design process by studying how structural design analysis guides mesh generation and how mesh geometric constraints affect design forms and structural systems.


Planar hexagonal mesh(left) & conical mesh(right) on the same input Brep polysurface
History and precedents
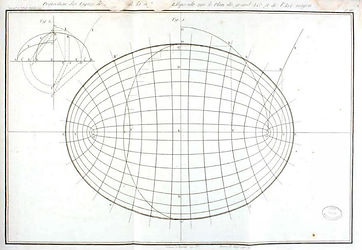

French mathematics Gaspard Monge used descriptive geometry to guide ellipsoid meshing with principal curvatures
Paneling optimization at Dondaemon design plaza (above, designed by Zaha Hadid Architect) and Stadium Sao Paolo(below, designed by Anibal Coutinho)

Deployment of shell structure in CNIT and its variation using a different network topology

Asymptotic grid shell, researched by Eike Schling.

Conical mesh with torsion-free support. Yas hotel(left) and Smithsonian National Museum(right).
Fabrication constraints guided net optimization

Red pavilion at Wuzhen Internet Conference Center and its nexorade supporting network (photography from the author)
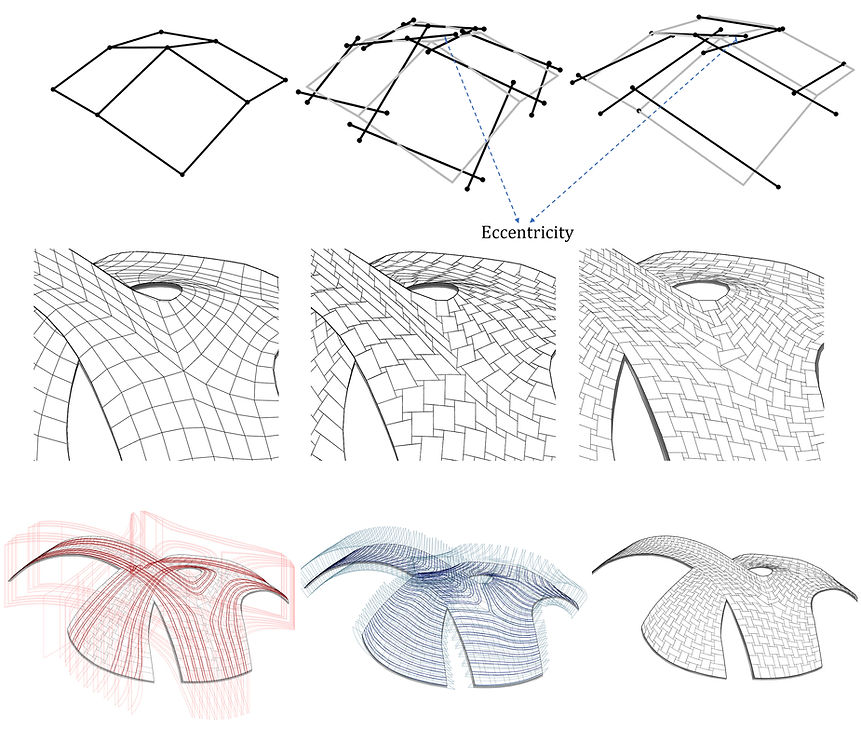
Diagram of supporting strip optimization based on the 3d-printing technique.

Initialize a conical mesh - 1. Convert input Brep to a dense triangle mesh; 2. Design a smooth power coordinated vector field on the mesh; 3. Integrating for a seamless parameterization and extract isolines; 4. Dualization for the quad/hex mesh
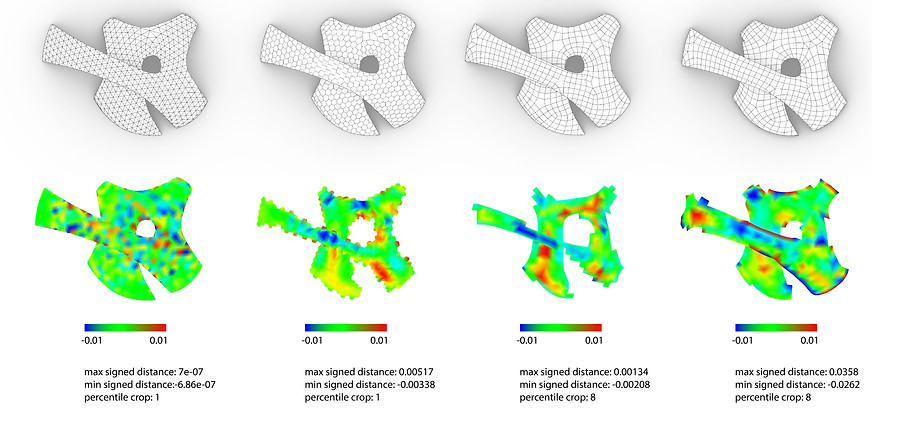
Optimize a conical mesh - After the initialization, we manipulate all the geometric constraints for the conical mesh as an objective. Then, we solve the unconstrained quadratic optimization using Newton's method.
Structural awareness guided net optimization

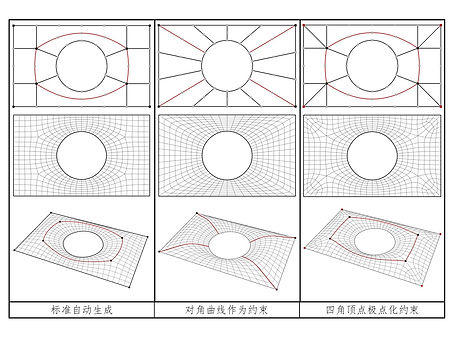
Topological net for the free-form surface. (From up to bottom) Human operation; the proposed boundary-skeleton-singularity-subdivision pipeline ; extra point constraints
Optimize a topological net with geometric feature constraints. (From left to right) No specific features; special guideline; polarized corners

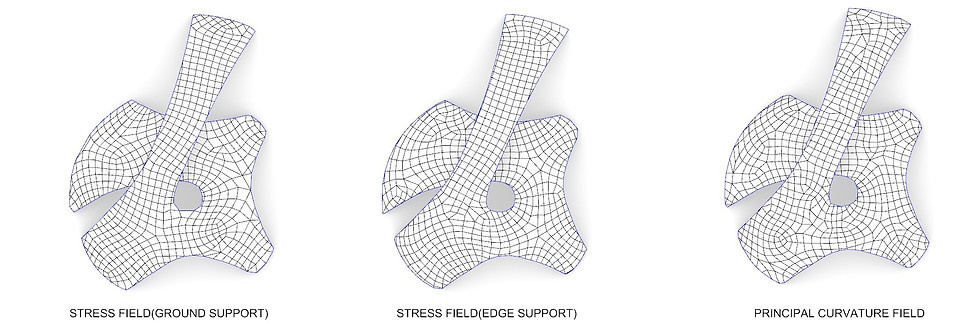
Stress field guided quad meshes. (From left to right) Anchors on the corners; anchors on the edges; principal curvature
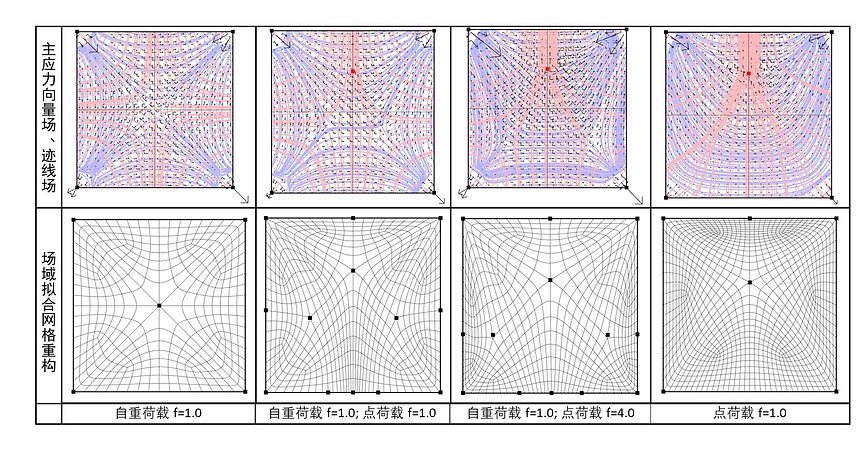
Reconstruction of the topological net from multiple loading conditions. The extra points are set to align with the stress field