XSHELL
PAPER SHELL MADE OF CELL UNIT
ELECTIVE COURSE, FALL '19, CORNELL UNIVERSITY
IN COLLABORATION WITH YU SUN, MENGYI YAN, AND JUNSIK OH
XSHELL
PAPER SHELL MADE OF CELL UNIT
ELECTIVE COURSE, FALL '19, CORNELL UNIVERSITY
IN COLLABORATION WITH YU SUN, MENGYI YAN, AND JUNSIK OH
This project explores the simplest way of constructing a doubly-curved shell structure - by setting the fabrication method based on planar manufacture, which can be achieved by CNC Routers or laser machines and using sheet materials like chipboard. The cellular unit was mapped and unrolled to planar folding and cutting lines, fabricated through tens of recycling chipboards within 2mm thickness. The whole fabricating process including cutting, folding, and assembling took only 5 days and 3 group members to complete the construction of this human-scale installation on the 3rd floor of Sibley Hall.
This project explores the simplest way of constructing a doubly-curved shell structure - by setting the fabrication method based on planar manufacture, which can be achieved by CNC Routers or laser machines and using sheet materials like chipboard. The cellular unit was mapped and unrolled to planar folding and cutting lines, fabricated through tens of recycling chipboards within 2mm thickness. The whole fabricating process including cutting, folding, and assembling took only 5 days and 3 group members to complete the construction of this human-scale installation on the 3rd floor of Sibley Hall.
BISTABLE AUXETIC SYSTEM
PROGRAMMING SYNCLASTIC CURVATURE INTO 2D PATTERNING
MASTER'S THESIS RESEARCH, 2020, CORNELL UNIVERSITY
The research aims to provide a new idea towards the ever-expanding question in architecture to construct free-form geometry. Rather than relying on formwork, the proposed reconfigurable system which translates free-form synclastic surfaces to pre-programmed pieces can be easily assembled in a flat state and then actuated to the given design requirement.
OVERVIEW
Auxetic materials are specific mechanical metamaterials, which have a negative Poisson’s ratio. Material with auxetic properties expand in the lateral direction when stretched and contract when compressed Poisson's ratio can govern the material's Gaussian curvature when bending, positive Poisson's material like rubber deforms into an anticlastic saddle-like shape when stretched; on the other hand, the auxetic material can produce synclastic curvature. This research reveals the insightful relationship between the flat and curved configuration for a certain type of auxetic pattern - bistable auxetic.

Flat-to-curve reconfiguration with stretching stress

Flat-to-curve reconfiguration with compressing stress

INITIATIVE
The pattern of the bistable auxetic system was first proposed by Rafsanjani and Pasini in 2015. At that stage, it was a pure planar system with the ability to stay on two self-stable configurations: either open or closed. I added tweaks on the hinges so that they incline towards the base plane, resulting in out-plane transformations.

(up) bistable auxetic patterns with calibrated hinges
(down) reference mesh rotations around implicit axes

Mindflow to build up the flattening process


Naive prototypes with the same skewing angle everywhere lead to an out-plane rotation as a system.

Naive rotation animation with same skewing angle in unit prototype
CONSTRAINTS
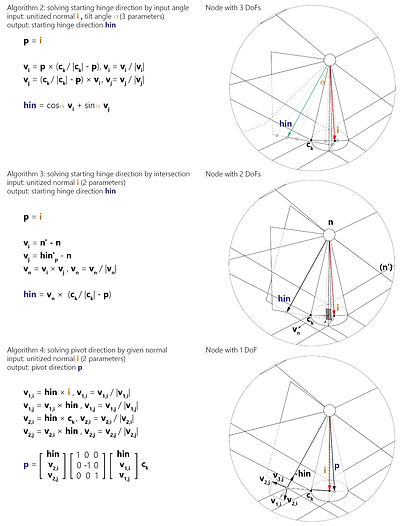
Given the original pattern, one can find that there are strong constraints within each node and around its vertex star. In fact, the bistable auxetic pattern limits the angle between rotators and their corresponding panels to only three degrees of freedom, and once one of its neighborhood's locations is defined, the DoF will reduce by one. These constraints also lead to the conicality lemma, ensuring that the hinge location can go back to its original place after a loop of rotation(also known as trivial connection).
ALGORITHM
An algorithm based on C# and Grasshopper was developed in order to transform free-form target mesh geometry to this proposed pattern that can be fabricated in a planar context. The pattern is actually a modified reciprocal structure with the ability to support self-weight, making it possible to serve as a flexible formwork with construction convenience.



Angle complimentary constraints
Axes coplanarity constraints
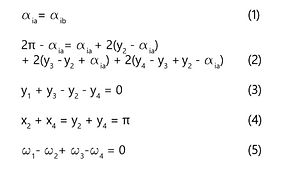

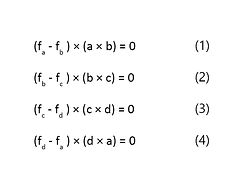
Conicality lemma

Decomposition diagram of the proposed system
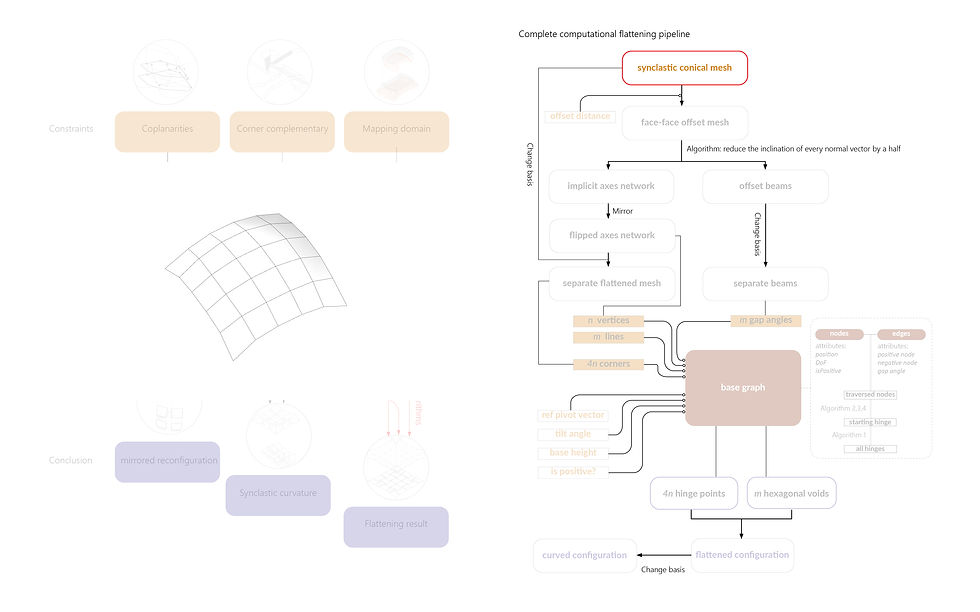

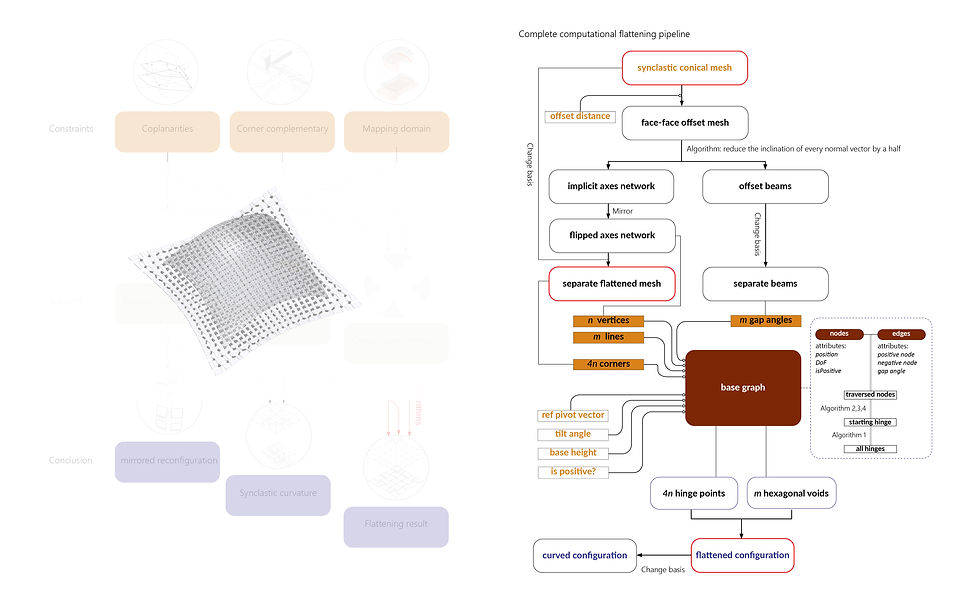

Algorithm flowchart demonstrating the pipeline behind the code

Physical simulation of the actuation for this system.
DESIGN INPUT GENERATION
One prerequisite for the input mesh is that it must be a conical mesh. It was proved that the angle relationship within each vertex provided by a conical mesh can solve the potential over-constraints in the generating process, giving one more degree-of-freedom in each vertex. I hereby give a method of creating such mesh with the help of the discrete tangential sphere. This method can be used for exploring design possibilities.

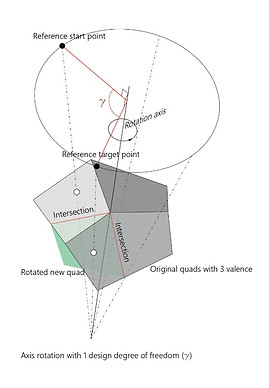
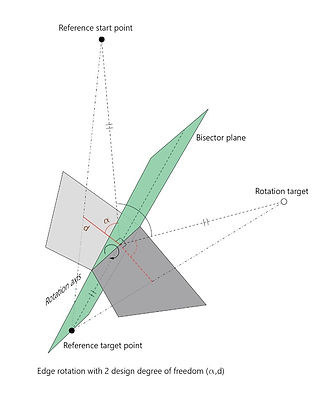
Mesh modification by rotating on a vertex
Mesh creation by building tangential faces of a unit sphere and parallel offsetting
FABRICATION AWARENESS
Models with various materials were tested to materialize the system and prove its feasibility. The most successful one was one that made of 4mm Polypropylene. The cuts made by CNC machines perfectly matches the calibrated gap, which programs the information of potential curvature. The most scalable one for construction was one that made of wood - both plywood and basswood - to fit with the mechanism and structural behavior of different parts of the system.


Model prototype made by 4mm polypropylene and the edge thickening steps to accompany with the CNC drill width
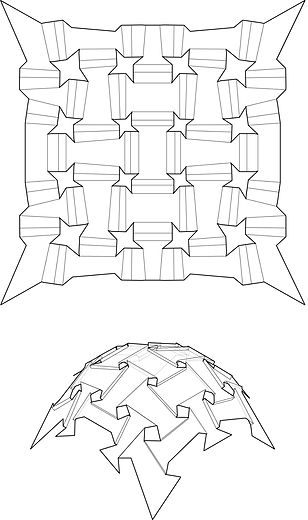

Model prototype made by paper and Kirigami



Model prototype made by wood and the decomposition of the engineered system
APPLICATIONS
This proposed system can be utilized in various contexts. The most obvious one is to use it directly as building components and to build dome-like pavilions or shelters. But the fascinating and applicable one is that it can be seen as a cheap and fast deployable formwork for large-scale vault construction. The Guastavino-like pattern provides both engineering efficiency and aesthetic quality. Another viable application can be in the field of dynamic screen system, where the bistable mechanism can provide switch behavior for energy-saving.


One potential application of this system: a falsework for Guastavino vaulting


Other potential applications of this system: a fast-deploy pavilion(left); responsive screen facades(right)
APPENDIX1: KEY PSEUDOCODES
APPENDIX2: GEOMETRIC INTERPRETATION OF HINGE_SOLVE ALGORITHM